原文發表於第 11 屆 iT 邦幫忙鐵人賽 (https://ithelp.ithome.com.tw/articles/10217180)
在夏末的傍晚,突然想用電腦算個圓周率

說算就算,原理什麼的先不管~我們在上一篇中已經安裝好 Anaconda 了,好想趕快寫點 python 啊!在維基百科上找到 Bailey–Borwein–Plouffe formula 公式,據說可以用來逼近圓周率。

Stack Overflow 論壇上則有別人寫好以 python 實作的程式碼。把程式碼複製起來貼到記事本中~
from decimal import Decimal, getcontext
# 引入需要的工具
getcontext().prec=100
# 設定精確度,要到小數點後第幾位
print(sum(1/Decimal(16)**k *
(Decimal(4)/(8*k+1) -
Decimal(2)/(8*k+4) -
Decimal(1)/(8*k+5) -
Decimal(1)/(8*k+6)) for k in range(100)))
# print() 的功能是印出括弧中的東西
# 括弧中的東西看來是表示上面的 BBP 公式
密密麻麻擠在一起,還有被誤判為錯字標上紅底線的函數名稱,整個更看不懂了,不過可以從 # 後面的中文大概猜到他每一行的功能~# 是註解的意思,代表其後的文字並不是要給 Python 執行的代碼,是給人閱讀的。將純文字檔案儲存檔案於桌面,記得把檔名存成 BBP.py,代表他是可以用 python 執行的,小心後面不要被作業系統偷加 .txt。

然後開啟終端機,cd Desktop 到桌面,輸入 python3 BBP.py,意思就是我們用 python3 來執行叫做 BBP.py 的檔案,終端機回傳計算的結果。

Yeah~下次點飲料之前可以先講一百位的圓周率了

(截圖來自【狠愛演】3分鐘成為學問教父,幹話小教室『大家學起來』)
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117070 去冰無糖綠茶
小數點後一百位不足以顯示我們對知識的追求,好想知道圓周率第一百萬位數到底是多少~於是回到記事本中稍做修改。

記得儲存純文字檔案,再回到終端機再次執行,在終端機中可以簡單地按 ↑ 方向鍵來回顧上一個執行的指令。

於是我知道圓周率的第一百萬位是 3,待會可以安心地吃宵夜了~
以上就是最基本最直接執行程式碼的狀況,但是在終端機中執行的話,一百萬位數的圓周率很難複製,這樣子我沒有辦法把他複製之後印出來背誦,沒有背誦圓周率我睡不著~
這麼棒的圓周率怎麼可以只用終端機執行,讓我們歡迎 Jupyter Notebook
如果我們改為使用 Jupyter notebook 的話,就可以在行間 (inline) 執行程式碼,馬上確認結果是否符合需求。請打開上一篇中已經安裝好的 Anaconda,點選 Jupyter Notebook 的 Launch。

終端機視窗會自動跳出來,莫急莫慌莫害怕,再等一下下瀏覽器視窗就會開啟進入 Jupyter Notebook,其上顯示著當前所在的資料夾位置,請自由地找到喜歡的位置之後,按右上角的 New ⇒ Python3。

新視窗跳出一個全新的程式筆記本,上方標題名稱 Untitled1 可以自由更改,點擊 Untitled 就可以修改為 BBP_python 的自訂名稱,一切自動儲存。

把剛剛的圓周率計算程式碼複製進第一個綠色框框中,綠色框框就是一個 cell,cell 可以放程式碼並執行,或是放 Markdown 格式的文字。複製到 cell 之後,按下 Ctrl+Enter 就可以執行那一個 cell 內的程式碼。

程式內容與執行結果是分開的,不怕失控!當然,一百萬位還是稍微多了一點~
最後還想要把一開始在維基百科看到的美美數學式加上去,新增一格 cell,並把 cell 的屬性改成 Markdown
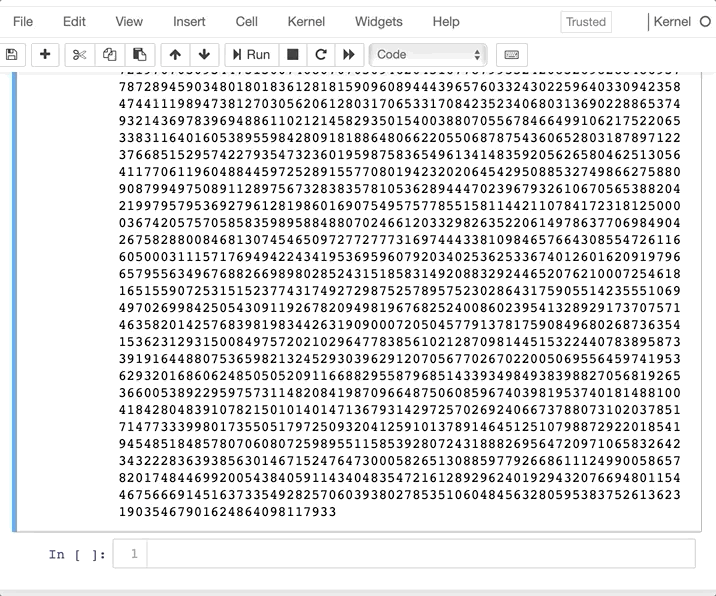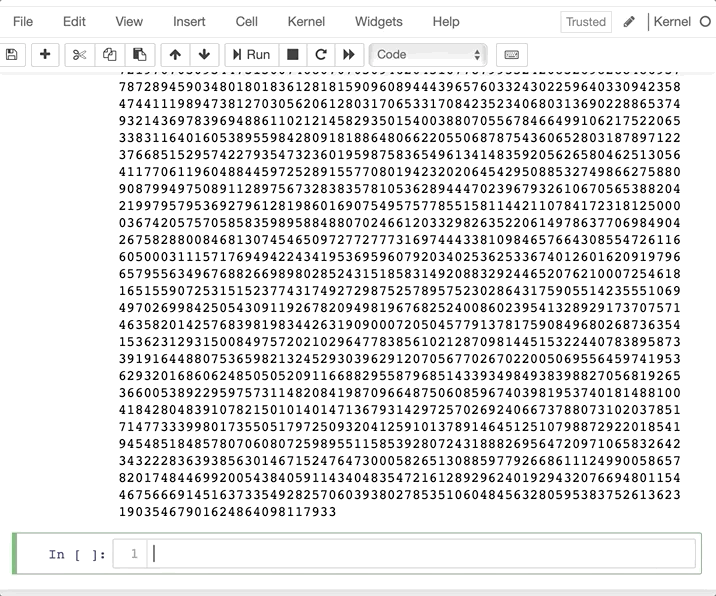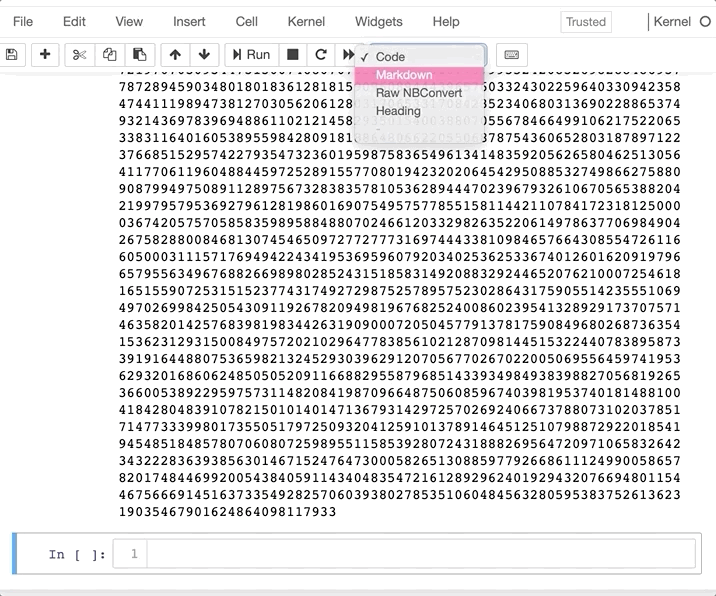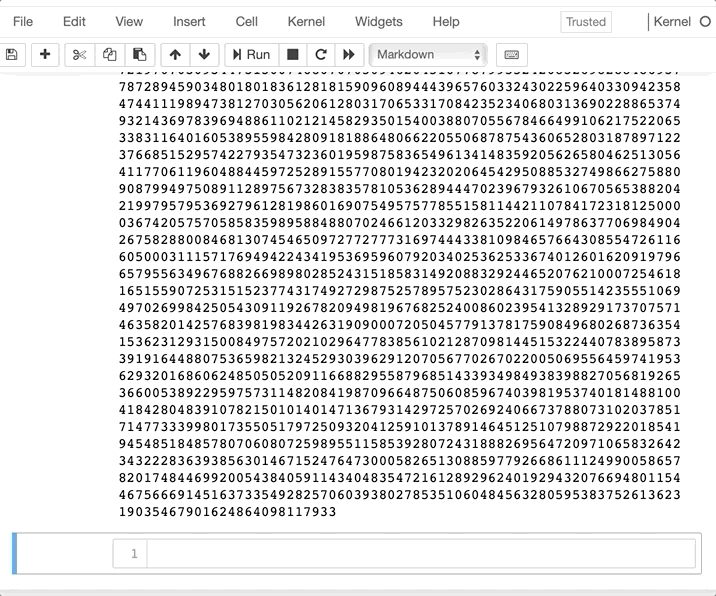
研究了一下數學式的表示方式之後,只要將下列的數學表達式:
$\pi = $$\sum_{k=0}^{\infty}$$[\frac{1}{16^k}(\frac{4}{8k+1}-\frac{2}{8k+4}-\frac{1}{8k+5}-\frac{1}{8k+6})]$
貼到新的一格 cell 中,再按下 Ctrl+Enter 就可以看到 BBP 公式 render 出來囉!

如果需要編輯的話,只需要雙擊數學式就可以回到編輯模式。
比起軟體開發工程師,進行生物資訊分析的資料科學家比較需要這種在行間執行一小段腳本的功能,以及行間比較不同格式的註解。下一回我將介紹另一種在純文字編輯器中進行互動式行間執行程式碼的方法~
參考資料與延伸閱讀
https://en.wikipedia.org/wiki/Bailey–Borwein–Plouffe_formula
https://stackoverflow.com/questions/28284996/python-pi-calculation
